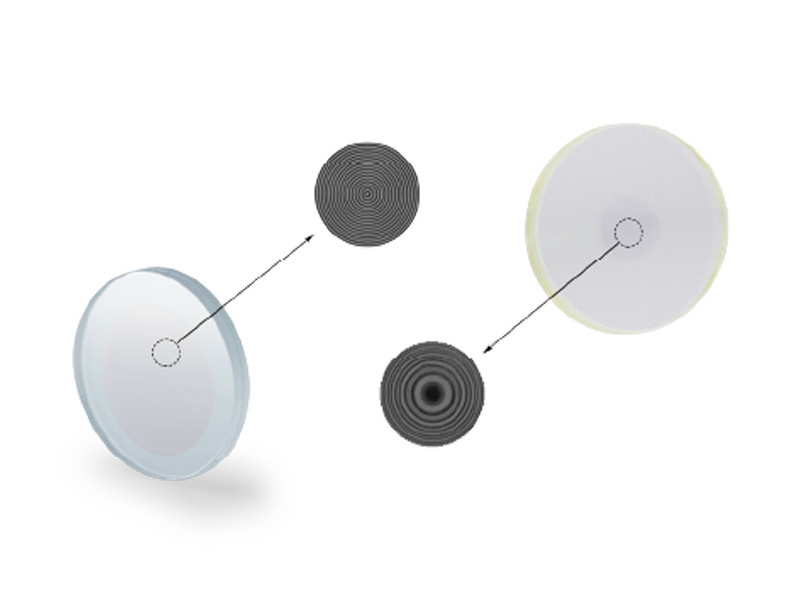
DOE光学元件之高斯光束的传播
理论和实践已证明,在可能存在的激光束形式中,最重要且最具典型意义的就是基模高斯光束。无论是方形镜腔还是圆形镜腔,基模在横截面上的光强分布为一圆斑,中心处光强最强,向边缘方向光强逐渐减弱,呈高斯分布。因此,将基模激光束称为高斯光束。
激光束腰和分布
为了获得高斯光束光学的精确原理和限制,有必要理解激光束输出的特性。在TEM(横模和纵模为0)模式下,光是从激光开始辐射,就像一个含有高斯横截发光剖面的完美平面波,高斯形状被激光内部的尺寸或者某种光学序列的限制光圈在某个直径处被截断。为了指定和论述激光光束的传播特性,我们必须给它的直径下一些定义。普遍被采用的定义是光束发光(最强烈)峰值,轴向或者数值的地方的直径衰减1/e2(13.5%)。
束腰,是指高斯光绝对平行传输的地方。半径,是指在高斯光的横截面考察,以最大振幅处为原点,振幅下降到原点处的0.36788 倍,也就是1/e*e 倍的地方,由于高斯光关于原点对称,所以1/e*e 的地方形成一个圆,该圆的半径,就是光斑在此横截面的半径;如果取束腰处的横截面来考察,此时的半径,即是束腰半径。沿着光斑前进,各处的半径的包络线是一个双曲面,该双曲面有渐近线。高斯光束的传输特性,是在远处沿传播方向成特定角度扩散,该角度即是光束的远场发散角,也就是一对渐近线的夹角,它与波长成正比,与其束腰半径成反比,计算式是:2*波长/ 3.1415926*束腰半径),故而,束腰半径越小,光斑发散越快;束腰半径越大,光斑发散越慢。

衍射效应使光在传播过程中向横向传播。因此它不可能有一个被精确校准的光束。激光光束的传播可以被纯衍射理论精确地预测。异常现象小到在这里可以统统不用去考虑。在非常平常的情况下,光束传播可以小到被忽略。下面的方程精确地描述了光束的传播,由此可以很容易地看出激光光束的能力和限制。

近场和远场的分别
不像常规的光束一样,高斯光束不是线性的分布。靠近激光的时候,分布角度是非常的小的。远离激光的时候,分布角如上描述接近渐进的限制。定义为光束半径通过2的平方根因素传播的距离,在下面式中给出

在光束腰(z=0)的地方,波阵面更加平坦。同样地,在z=∞处,波阵面也更加平坦(R(∞)= ∞)。随着光束从腰部传播,波阵面的曲率因此必须增加到最大值并且紧接着开始下降,如下图所示。Raleigh范围,考虑到在近场分布和中波段分布之间的区分线,是从波阵面曲率最大值腰部的距离。远场分布(数值查询激光器说明)必须在远大于ZR(通常大于10nbsp即足够)的时刻才能别测量。这是非常重要的区别,因为在一个光学序列中对点大小和其它参数的计算会在近场或者中场分布被使用时变得不准确。对于一个紧紧被聚焦的光束,从腰部(聚焦点)到远场的距离仅仅是几毫米或者更小。对于从激光直射光束,远场距离可以按米的数量级来测量。


董事长陈义红博士在新加坡分享创新创业经验

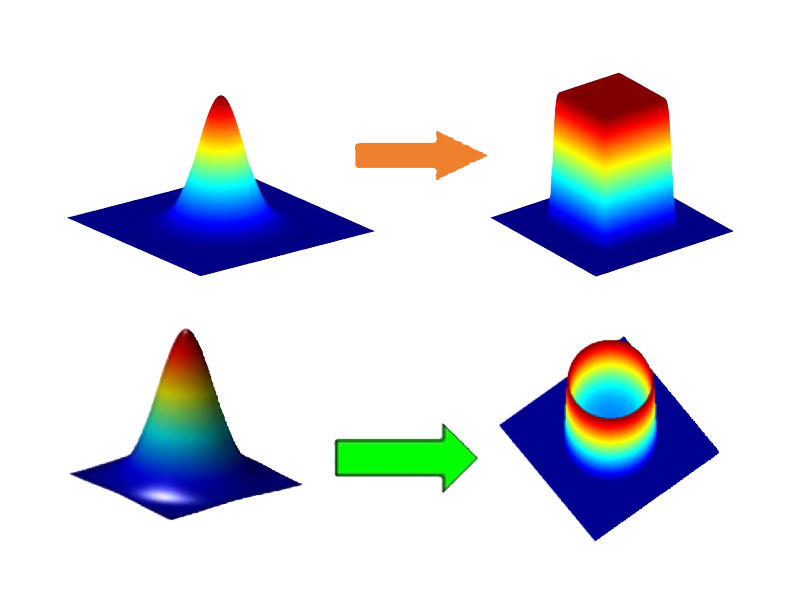
平板锥透镜简要介绍及典型应用案例

激光模式转换器简要介绍及其典型应用案例
艾里光束转换器简要介绍及其典型应用领域

简要介绍涡旋波片及其典型应用领域

简要介绍迷你型二维音圈扫描镜(电动二维扫描镜)及其应用领域

衍射光学元件(DOE)在激光材料加工中的应用

简要介绍可变焦莫尔透镜